
The Marine Mammal Observer Association (MMOA) is pleased to present this Distance Estimation using Reticular Binoculars help guide in response to enquiries from our international membership. Given the prevalence of conflicting information on the internet, we recognised the need for a resource to address questions surrounding this vital aspect of marine mammal observation. We trust that this resource will serve as a valuable reference and contribute to the proficiency of marine mammal observers worldwide.
Reticular binoculars and scopes estimate the distance to targets for shooting or objects such as lighthouses at sea. These binoculars would historically use slightly different range measurements for reticles with 6,283.185 milliradians in a circle (think of the circle as the earth). But essentially, they all measure the angle below the horizon for range determination when working as a marine mammal observer (MMO).
Some binoculars, such as the Hawke reticular binoculars, give angle measurements in milliradians. This is probably simpler than using reticles, which causes some confusion for some people, and there are a standard 10 milliradians per reticle.

Hawke range finding binoculars in milliradians (Hawke Optics Ltd)
The Bushnell 7x50 Marine binoculars (model 137500) manual states that each mark on the vertical scale is equivalent to 5 mil. But note that there are full reticle (10 mil) and half reticle markers (5 mil). The exact division used can be down to the manufacturer, and these are often described in the manual. The manual for the Pentax Marine (7x50) describes the reticle use clearly “Each minor division on the horizontal scale and vertical scale indicates 5 mils and each major division indicates 10 mils” (see: https://www.bhphotovideo.com/lit_files/517692.pdf ). This statement holds true for every pair of binoculars I have come across but there may be others it doesn’t apply to.
Now that you have correctly determined how to count the number of mils from the horizon to your target you need to determine how to calculate the distance. Typically this is done with a very simple calculation as follows:
Eye height (m) x 1000/mils
This is considerably simpler than the Heinemann (1981) equation used by the JNCC for the rangefinder stick 9 https://data.jncc.gov.uk/data/e2a46de5-43d4-43f0-b296-c62134397ce4/Guide-making-rangefinder-stick-rev01-Web.xls ) and introduces overestimation of distances, which increases with distance, with larger distances producing greater error margins and somewhat defeats the purpose of using reticular binoculars in the first place. Applying the Heinemann equation, we can see more accurate results.
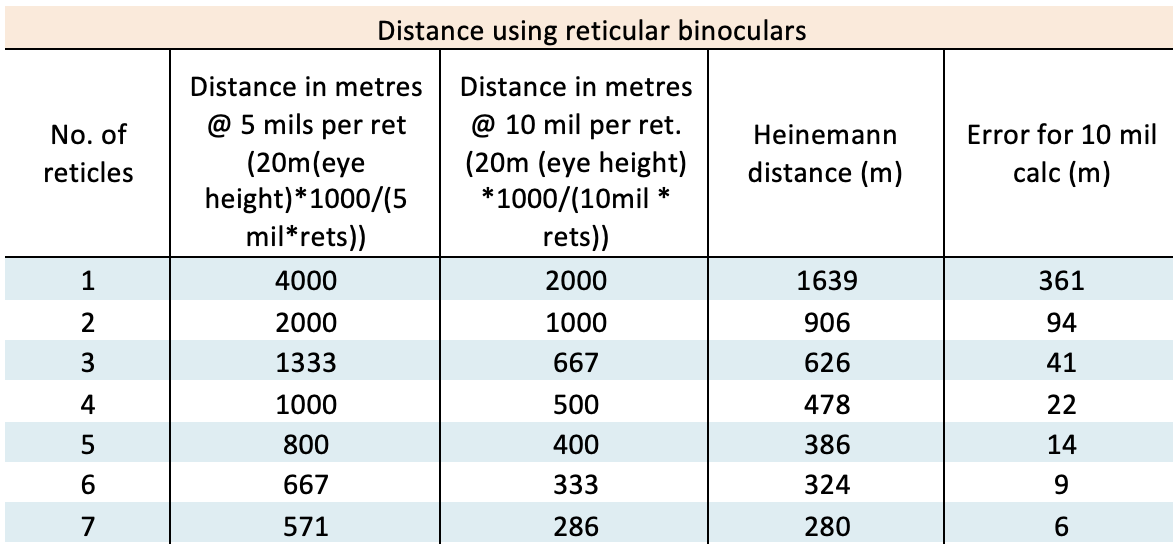
Comparison of distance estimation calculation for eye height of 20m.
If you count your number of mils incorrectly, this will produce a very large error. The Heinemann equation as used by the JNCC rangefinder stick is a little complicated and has been used in the attached spreadsheet. Distance to the horizon is based on eye height and calculated the same way as the JNCC. The calculation used can be seen by placing your cursor over the relevant cell; however, only white cells can be changed, and coloured cells are password-protected to stop accidental changes. The radius of the earth changes approximately 21 m from equator to pole and has a negligible influence on calculations. Lerczak and Hobbs (1998) produced a more accurate method of calculating the distance, but it is less precautionary, and the differences are very small.
The spreadsheet also allows the calculation of the distance to the source on the right side. Distance from gun array to observer typically doesn’t change often, and the angle should be the angle from you to the animal with your back to the source. So typically, this angle is off the bow of the survey vessel, but this is assuming the source is 180 degrees behind the vessel. Once the number of reticles (1 ret= 10 mil) is entered the spreadsheet gives you distance to animal and from animal to source.
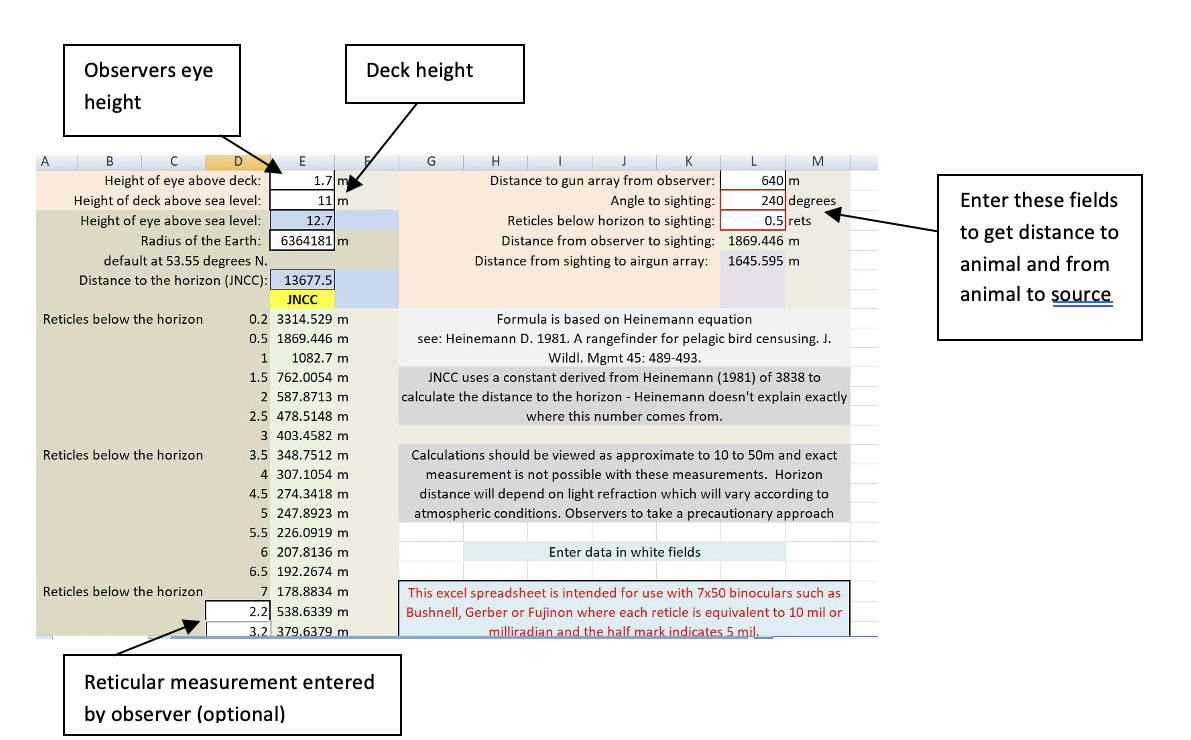
Spreadsheet fields for distance estimation.
References
Heinemann, D., (1981), A range finder for pelagic bird censusing, The Journal of Wildlife Management, vol. 45, no. 2. Pp 489-493.
Lerczak, J.A., and Hobbs, R.C., (1998), Calculating Sightings distance from angular readings from shipboard, aerial and shore-based marine mammal surveys, Marine Mammal Science 14(3); 590-599; see also Errata in vol 4, pg 903.

